二 等辺 三角形 比 364920-二等辺三角形 比率

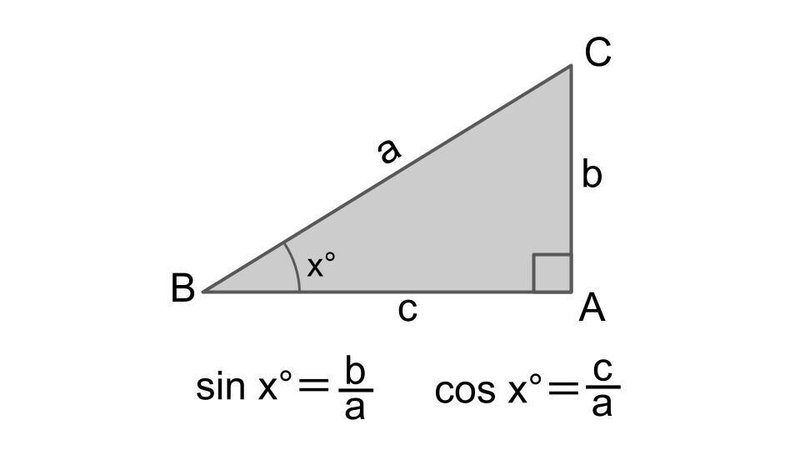
Sin Cos Tan で手計算で計算できるものまとめ 数学の偏差値を上げて合格を目指す
こんにちは、ウチダです。 今日は数学a「図形の性質」で習う 「三角形の内心」 について、性質の証明や基本的な使い方(角の二等分線と比)、座標の求め方や位置ベクトル表示などをわかりやすく解説していきたいと思います。 外心に関する記事と内容がか 二等辺三角形ではない三角形を思い浮かべてください。 いろんな三角形が思い浮かんだと思いますが、その中に正三角形はありましたか? ないですよね? すなわち 二等辺三角形ではない ならば 正三角形ではない これは今、想像してもらった通り真です。
二等辺三角形 比率
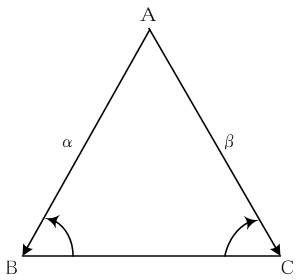
二等辺三角形 比率- 今、二等辺三角形が熱い! ~小学校の算数が懐かしい デイリーポータルZ 21年5月31日 自分が小学生時代に流行ったマンガやアニメ、おもちゃなどに触れると、懐かしむのみならず改めてハマってしまうことはないだろうか。 筆者は最近、で中学 三角比と角の二等分線 角の二等分線とは、角を同じ大きさに分ける線のことです。下の図で言うと、 AD が $\angle \mathrm{ A }$ の二等分線です。 有名な性質として、 $\mathrm{ AB }\mathrm{ AC }=\mathrm{ BD }\mathrm{ CD }$ になる、というものがあります。 次のように、 C を通り、 AD に平行な線をひくと
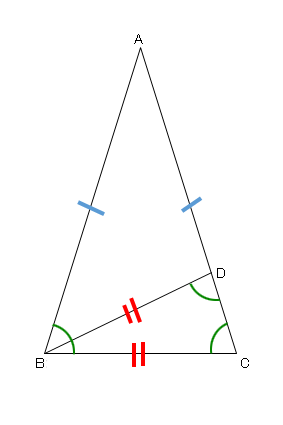
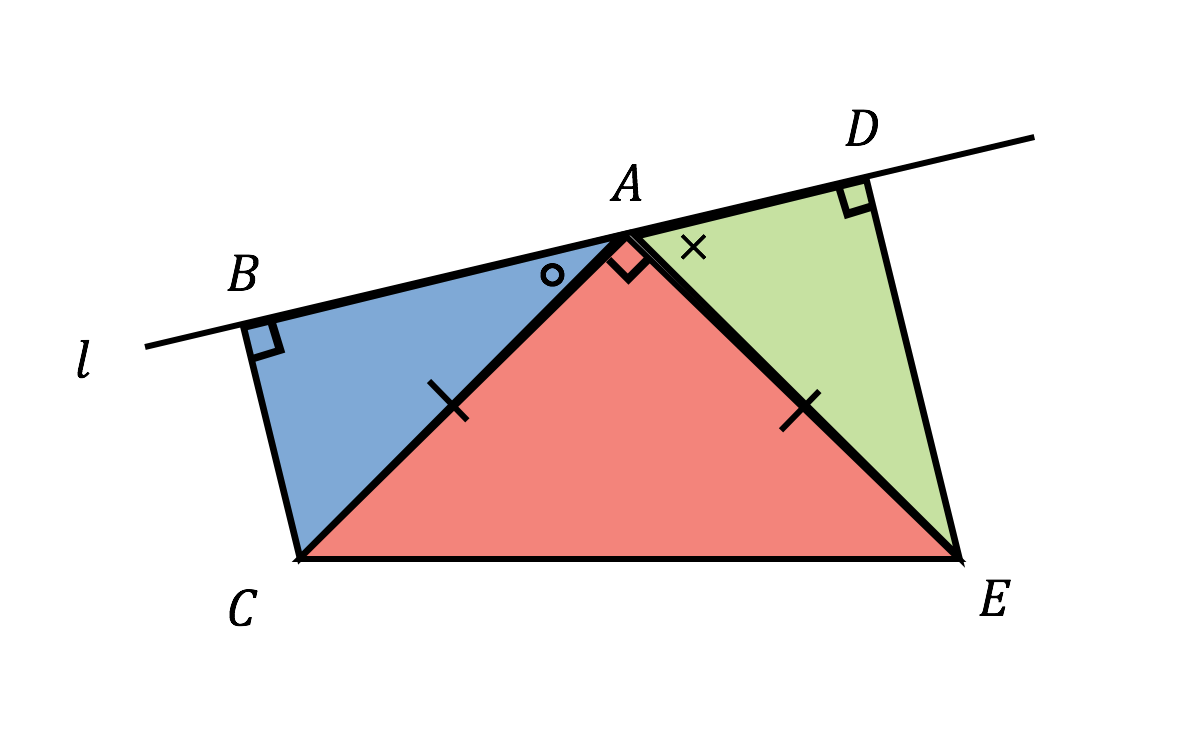
二等辺三角形の分割
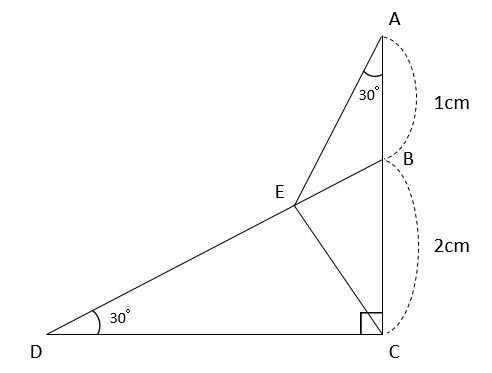
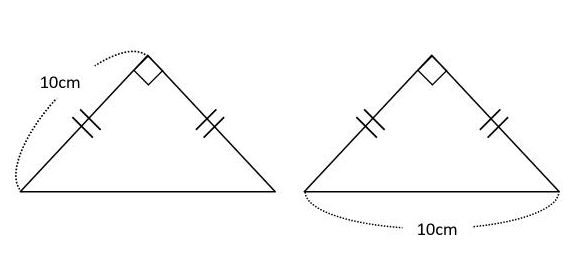
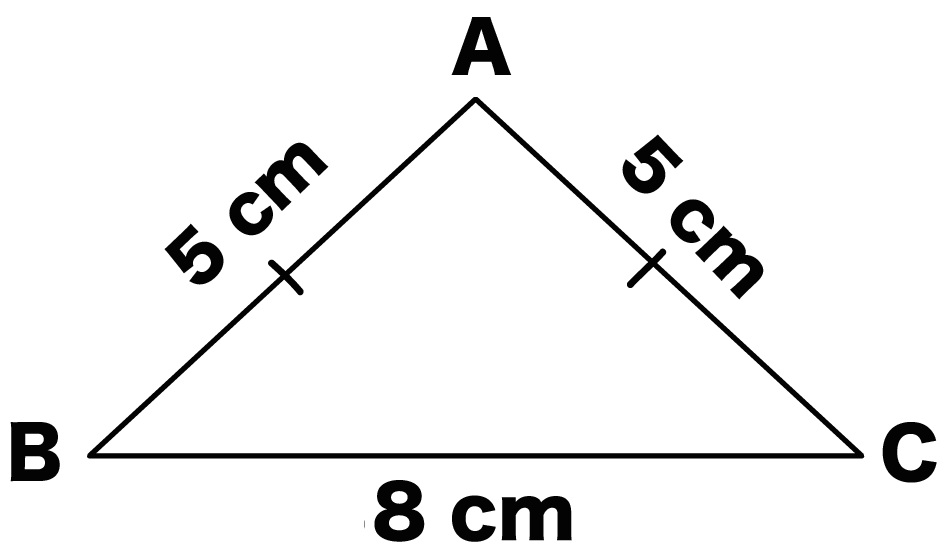
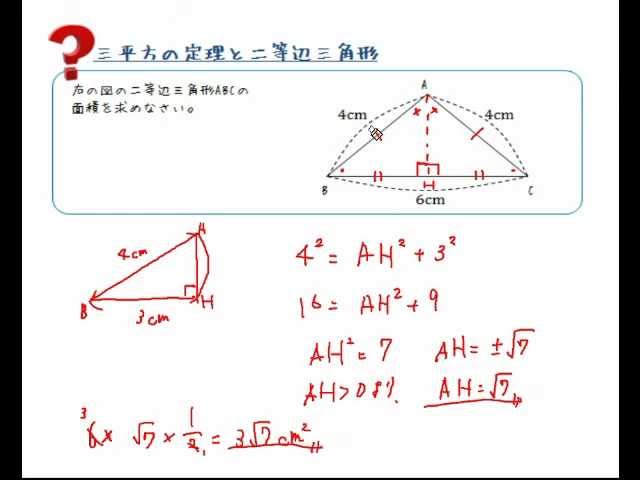
AB = √2BC = 5√2 cm;三角形の3辺が与えられたときの面積の求め方 「3辺の長さが,5,4,7の三角形の面積を求めよ。」という問題がわかりません。面積を求めるときは,公式 S=1/2bc sinA に当てはめればいいことは二等辺三角形(にとうへんさんかくけい、英 isosceles triangle ) 二等辺三角形の一辺から 直角に線 を引き、 高さ を作ります。 高さの長さを求める 補助線により出来た三角形は、 30°, 60°, 90°の直角三角形 です。 この 三角形は 一番長い辺と一番短い辺の 長さの比が 2 1 になっています。
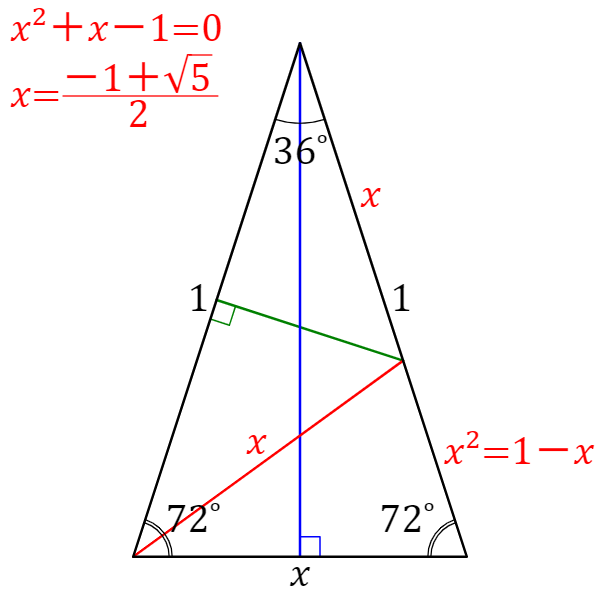
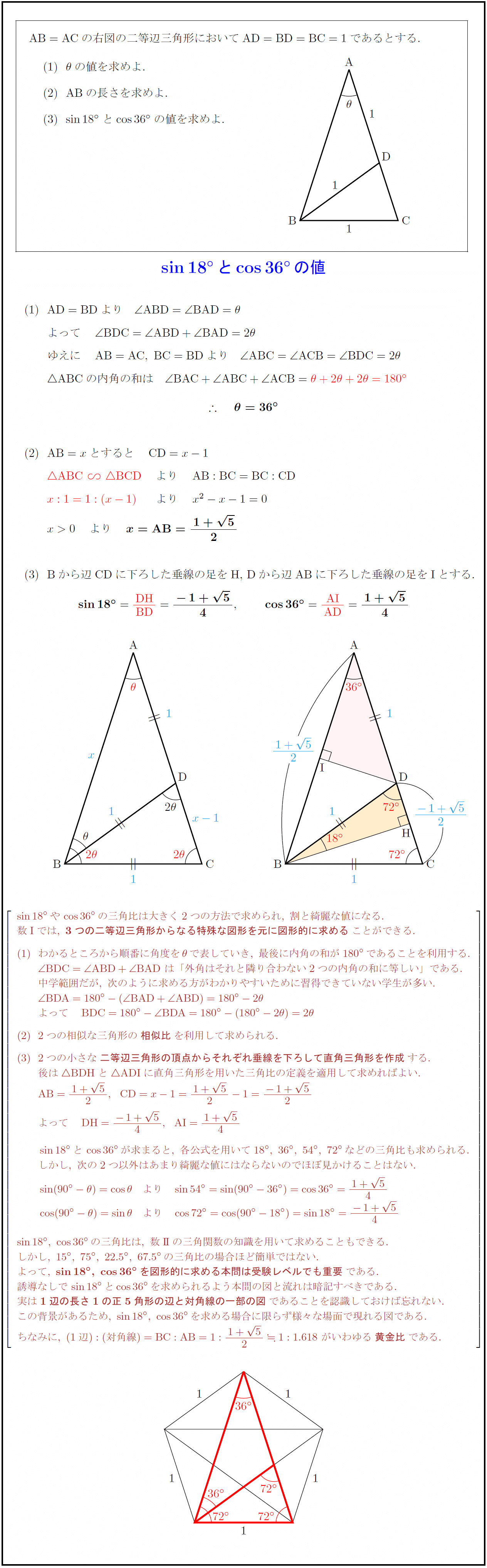
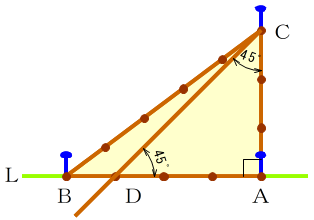
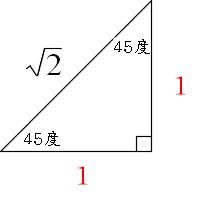
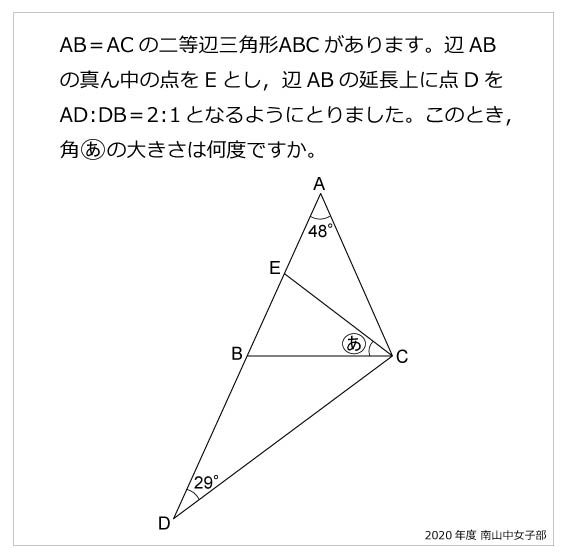
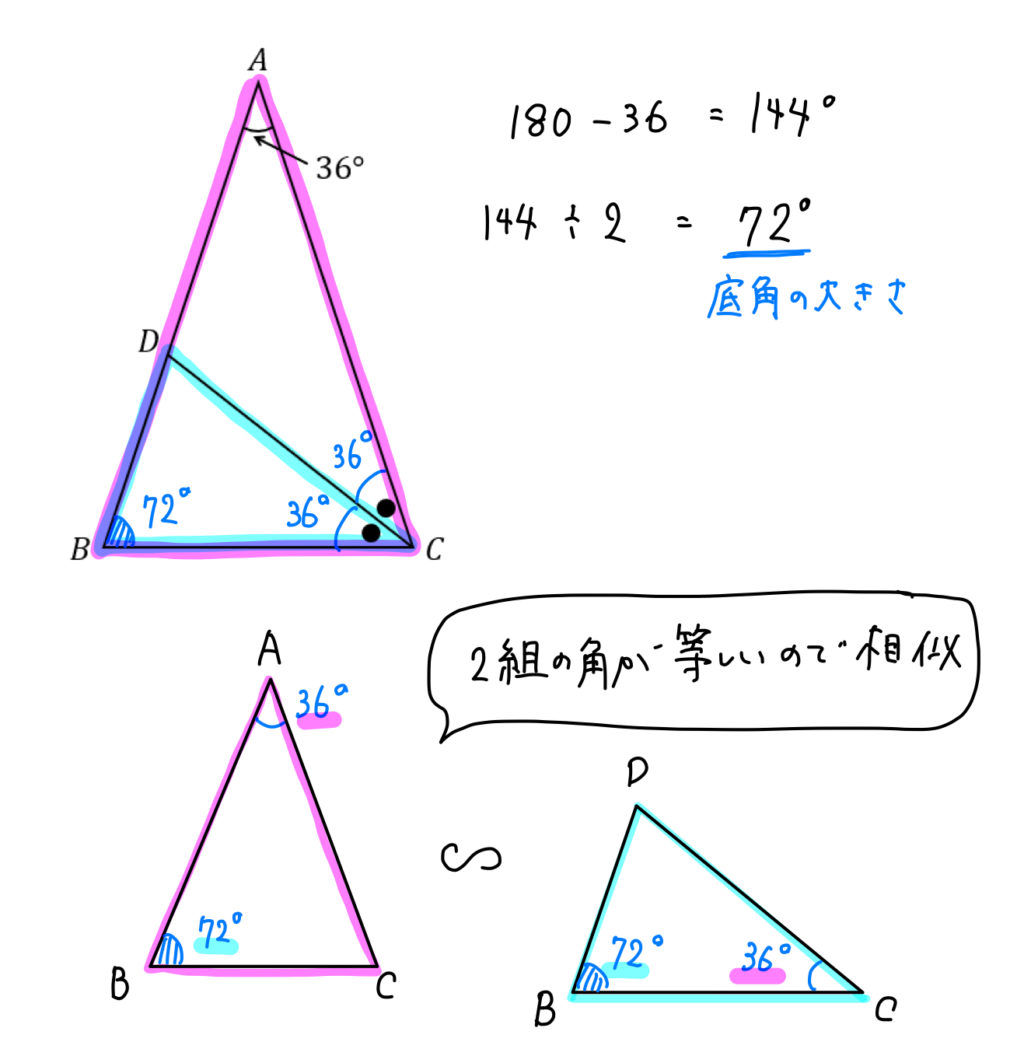
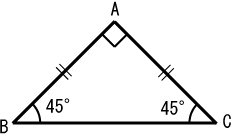
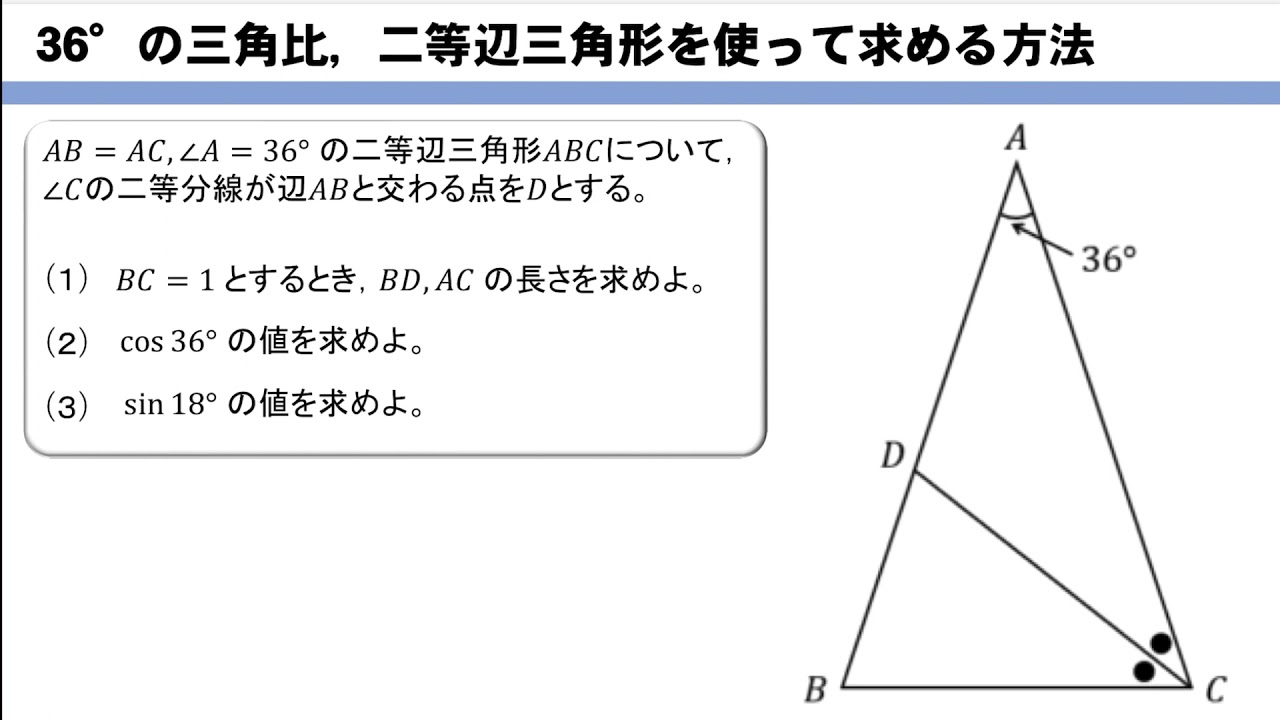
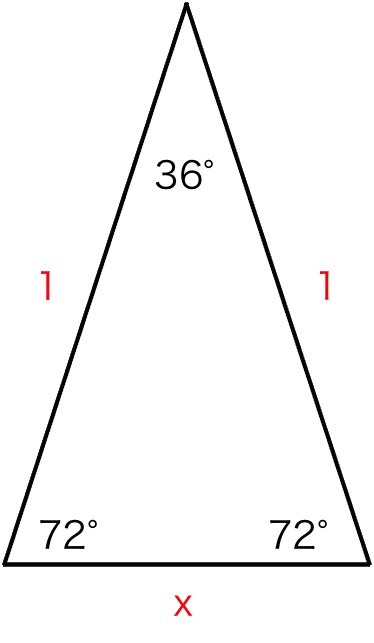
図5のように二等辺直角三角形の三角比は以下になる。 $$\sin45°=\cos45°=\frac{\sqrt{2}}{1}\\ \tan45°=1$$ 三角比の公式 三角比sin,cos,tanの間にはある関係がある。 それを公式をして理解することで三角比を変換をすることもできる。 (例えばsinからcosに 36度の三角比 次の図は、 $\mathrm{ AB }=\mathrm{ AC }$ の二等辺三角形 ABC をかいたものです。 $\angle \mathrm{ A }=36^{\circ}$ で、 $\mathrm{ BC }=1$ とします。今、 $\mathrm{ AB }=x$ とおいて、これを求めてみましょう。これがわかると、36度の三角比も求められるようになり 二等辺三角形の角度を求める問題を練習したいですっ★ ってことで、今回の記事では二等辺三角形の角度を求める問題について解説していきます。 角度を求める問題は、図形の性質を覚えてしまえば楽勝! だから、この記事を通して二等辺三角形
二等辺三角形 比率のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 | ||
 |  | |
 |  |  |
「二等辺三角形 比率」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「二等辺三角形 比率」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  | |
「二等辺三角形 比率」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「二等辺三角形 比率」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
「二等辺三角形 比率」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「二等辺三角形 比率」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  | |
「二等辺三角形 比率」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「二等辺三角形 比率」の画像ギャラリー、詳細は各画像をクリックしてください。
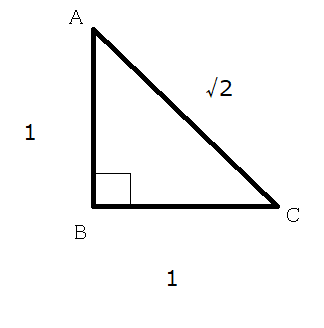 |  |  |
 |  |  |
「二等辺三角形 比率」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 |  | |
「二等辺三角形 比率」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「二等辺三角形 比率」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | 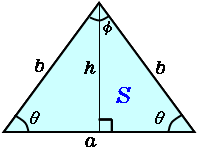 |
中点 したがって efgは二等辺三角形となる。 確認 四角形abcdで、p,rはそれぞれ辺ad, bcの中点、q,sはそれぞれ対角線bd,ac の中点である。 答表示 a bき,等辺:底辺 φ:2 である.黄金比が 最も美しい比であると言われるが,それに 倣えばこの比の二等辺三角形が最も美し い二等辺三角形であると言えるのだろうか.確かに,安定感を 感じる二等辺三角形ではあるのだが. $ % & 2
Incoming Term: 二等辺三角形 比, 二等辺三角形 比率,
コメント
コメントを投稿